When you use an Erlang C calculator or the more advanced Erlang X calculator, you get a relatively accurate need for the staff that needs to be on line. At the same time, it is clear that people are living beings, they periodically need to leave the workplace. And if they leave, then, accordingly, the proportion of lost calls (LCR, Lost Contacts Rate) during their absence increases, and the average speed of response (ASA, Average Speed of Answer) falls. Let's use an example to study how many people you need to have not on the line, but in the state in order to maintain the target response speed.
| Parameter | Unit rev. | Meaning |
| Call volume | sound/hour | 500 |
| Average processing time | sec | 200 |
| Target Average Response Rate | sec | twenty |
| Line schedule | – | 5/2 from 9:00 to 18:00 |
It is necessary that there are 32 operators on the line at the same time. Their load factor (Occupancy) will be: OSS = ( 250 x 200) / 32 x 1.800 = 0.87 , which can be considered an almost ideal result. 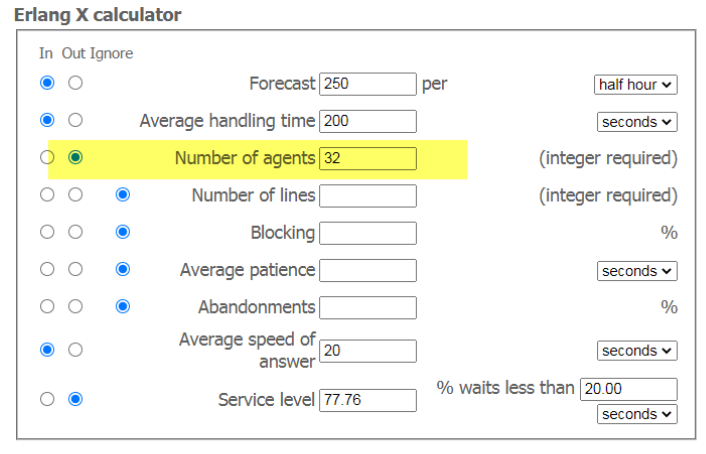 Since operators are absent for non-telephone activities, we must take this into account. The amendment is called CSS Utilization (or CSS UTZ for short). CSS UTZ= Total Time On Line / All Paid Time Let an operator's work day be from 9 am to 6 pm and have 1 hour of paid break.
Since operators are absent for non-telephone activities, we must take this into account. The amendment is called CSS Utilization (or CSS UTZ for short). CSS UTZ= Total Time On Line / All Paid Time Let an operator's work day be from 9 am to 6 pm and have 1 hour of paid break.
| Time spent per day | Quantity, hour | % of paid time |
| Break | 1.00 | 11.1 |
| Coaching with a supervisor | 0.25 | 2.7 |
| training | 0.25 | 2.7 |
| Random causes (unforeseen factors) | 0.25 | 2.7 |
| Meeting | 0.05 | 0.56 |
| Administrative matters | 0.05 | 0.56 |
| Downtime for technical reasons | 0.05 | 0.56 |
| Total | 1.90 | 21.1 |
CSS UTZ= ( 9.0-1.9) / 9.0 =0.789 The operator is available to handle calls 78.9% of billable time. Accordingly, it will take 32 / 0.789 = 40.5 FTE (full rates in the state) so that the guys can go on breaks and training. There is another factor that is usually not taken into account. This is an unplanned absence of operators from the workplace due to being late. It is necessary to make an allowance for lateness, in practice it is about 6% of the paid time. total need 40.5 / (1-0.06) = 43.1 FTE. This is not all, because the factor of the absence of people in the workplace is not yet taken into account. Reasons can be, for example, illness (unplanned absence) or vacation (planned absence).
| Days per year | Quantity |
| Disability due to illness | 14 |
| Vacation | 28 |
| Leave at your own expense | 5 |
| Other | one |
| Total | 48 |
Accordingly, taking into account the safety factor for personnel (48 / 365 = 0.13), the state needs to have 43.1 / (1-0.13) = 49.5 FTE. Now there seems to be enough people, but in fact – no. The fact is that there is a very unpleasant phenomenon, which is called the drift of the contact processing time (the same 200 seconds that were substituted into the Erlang calculator to calculate the need for operators). To put it simply, over time, processing contacts with a subscriber of the same complexity begins to take different times. On long horizons of time, for example, due to a change in the script of the conversation. And during the day it simply grows due to the accumulating fatigue of operators and subscribers. And it grows well, up to 30%. This means that a contact that took 3 minutes to process in the morning will take all 4 minutes in the evening. The need for operators due to drift will differ with the same call volumes, this must be taken into account. And that's not all. Additionally, it would be good to take into account the outflow of personnel, especially in contact centers, where the training cycle is long. For example, if employees leave on average once every two weeks, the probability of leaving on a given day is 1/14 = 0.07. The cost of risk is the product of its probability times the price, in this case losing 9 [billable hours] x 0.789 [UTZ]. In total, an additional 0.07 x 9 x 0.789 = 0.49 man-hours are needed on each working day of the line (a tautology, but correct: if the line works on weekends, then it is still impossible to quit these days) in order to have a margin of outflow. A total of 32 operators in the line turn into 50+ people in the state. In fact, if the non-peak hour were considered in the problem, one would also have to remember that there are about 1.4 times more calls in the busy hours than the “hospital average”. It is common to do the same calculation as above for the HNN and for the “normal” hour, and then take the average FTE between them so that there is not a whole surplus of operators. At the same time, remember that the Erlang calculation gives a small margin “from above”.


